回顾贝叶斯公式

February 6, 2022 by walter

盗墓贼的抉择

假设场景为盗墓，墓中情况不明，可能有宝物（概率为1/3），也可能有机关陷阱(概率为 2/3)，通过探测仪可以检测到机关陷阱，但是并不完全准确，对机械类的机关还行，对有毒的东西就难以检测出来了，检测的错误率为 1/4
那么盗墓贼通过分金定穴术，找到一个古墓，通过探测得知墓中没有机关，那么墓中其实有机关陷阱的概率有多少？如果概率小于30%，那么盗墓贼就决定准备点防护措施，冒险一试

以随机变量 X 表示墓中有机关的概率，有随机变量 Y 表示探测到机关的概率

已知：

• P(X=有机关) = 2/3
• P(Y=没发现机关 | X=有机关) = 1/4
• P(Y=发现机关 | X=没有机关) = 1/4

未知待求：

• P(Y=没发现机关 | X=有机关) 的概率

分析

• 2/3 的概率是有机关，1/4 的概率会检测错： (2/3)*(1/4) = 1/6
• 1/3 的概率是无机关，3/4 的概率会检测对： (1/3)*(3/4) = 1/4

所以没有发现机关的概率为 1/6 + 1/4 = 5/12, 其中X=有机关的概率是
(1/6)/(5/12) = 2/5 = 0.4 , 结果为 40%，这样盗墓贼最终还是决定这次就不冒险了，先回去买防毒面具和防弹衣

概率

概率是我们对一个事件发生与否的可能性的估计，这个估计如果还没有事实证明，我们称为先验概率(prior probability)，经过事实证明了，我们可称为后验概率(posterior probability)。

“实践是检验真理的唯一标准”，从实践中来，到实践中去，我们可以根据实践中的证明来修正甚至改变我们之前的假设和估计。

事件 B 所发生的概率记为 P(B), 称为先验概率，在验证之前的概率。

边际概率是事件的概率，与其他随机变量无关。如果随机变量是独立的，那么它直接是事件的概率，否则，如果变量依赖于其他变量，那么边际概率是事件的概率对因变量的所有结果求和，称为总和规则。

• 边际概率：事件的概率，与其他随机变量的结果无关。

联合概率是两个（或更多）同时发生的事件的概率，通常用来自两个因随机变量的事件 A 和 B 来描述，例如X 和 Y。联合概率通常被概括为结果，例如A和B。

• 联合概率：两个（或更多）同时发生的事件的概率，例如P(AB) 或 P(A, B)。

条件概率是在给定另一事件发生的情况下一个事件的概率，通常用来自两个因随机变量的事件 A 和 B 来描述，例如 X 和 Y。

• 条件概率：给定另一个事件发生的一个（或多个）事件的概率，例如 P（A given B）或 P（A | B）。

联合概率可以使用条件概率来计算；例如：

P(A, B) = P(A | B) * P(B)

这称为概率乘法公式。重要的是，联合概率是对称的，这意味着：

P(A, B) = P(B, A)

条件概率可以使用联合概率来计算；例如：

P(A | B) = P(A, B) / P(B)

条件概率不对称；例如：

P(A | B) != P(B | A)

条件概率

在事件 B 已经发生的条件下，事件 A 发生概率称为条件概率，记为 P(A|B), 且有

P(A|B)=P(AB)/P(B)

由此得概率的乘法公式为

P(AB) = P(B)P(A|B)
P(AB) = P(A)P(B|A)

全概率公式

全概率公式用于将一个复杂事件的概率分解成一些简单事件的概率之和，具体定义如下：

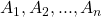如果事件组 两两互不相容，且 就称事件组 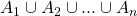构成了 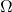的一个完备事件组。

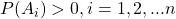若 , 则对于任何事件 B, 有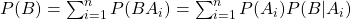

贝叶斯公式

• P(A|B) – B 事件发生条件下事件 A 发生的概率
• P(B|A) – A 事件发生条件下事件 B 发生的概率
• P(A) – 事件 A 发生的概率
• P(B) – 事件 B 发生的概率

贝叶斯公式很有用，我们常常有一个经验判断，大致判断事件 A 的发生概率 P(A) 是多少, 这个叫先验概率

在一定条件下，比如事件 B 发生的情况下，这个概率会怎么变化， 这就是贝叶斯公式要解决的问题

结合全概率公式

若 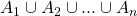为样本空间 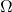的一个完备事件组，且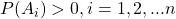，B 为满足条件 P(B) > 0 的任一事件，则

Note that events A and B are independent events (i.e., the probability of the outcome of event A does not depend on the probability of the outcome of event B).

Comments |0|